Classic descent planning usually includes a time/distance/rate algorithm worthy of space shuttle re-entry or a that-looks-about-right guess. The latter often results in a screaming, idle path that ends with, “Ahhh, Center, we’re gonna have a little trouble crossing STING at 3000.”
Wouldn’t it be neat if you had a ring-and-bead gun sight like the old Flying Tigers P-40s to point the nose and smoke your descent target? In a way, you do.
Any angle set by the pilot will yield a given rate of descent at a given speed. Your vertical rate verifies the airplane is pointed at the target, just like zero VSI verifies a level flight attitude. This philosophy is better known as control-performance instrument flying.
The run-of-the-mill glideslope is three degrees and, honestly, a comfortable en route descent is the same. But wait, you ask, how could I possibly set an angle while flying? The nifty protractor of the skies is called the attitude indicator; it accurately substitutes for that windshield bug smear your first CFI showed you back on ride one.
The only mental math you’ll need for this trick includes tripling a number, dividing a number in half or estimating a percentage of 10. To find the distance required, take the altitude to lose and triple it. This is the mileage you’ll need to get down. An easy example is 5000 feet to lose. Five times three is 15, so at 15 miles to go, lower the nose three degrees from whatever makes your level-flight pitch attitude, adjust power to maintain your speed and away you go. It’s a classic case of control producing performance.
In a perfect world, this is all you’d need, but things like changing winds and TAS, or sloppy piloting muddy the waters. To prove that you’re achieving a three-degree slope, cross-check vertical speed. Because we’re basing our descent on a stationary point, such as a fix or an airport, using groundspeed for all estimations is key, because it takes into account any and all variables.
Take your groundspeed, cut it in half and add a zero; that’s the required rate to maintain a three degree slope. For example, if GS is 100, half is 50 and with a zero tacked on is 500 FPM. Any more and you’ll get down too soon. Any less and you won’t get down soon enough. If you fly a faster machine, say 200 knots over the ground, then 1000 FPM is required. It’s that easy and this works in any airplane.
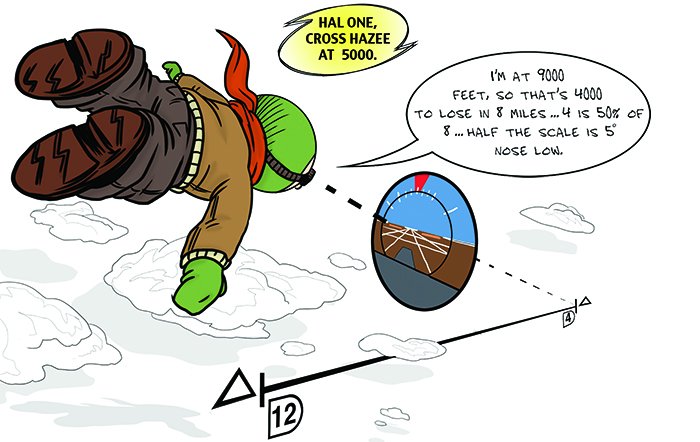
Now, not every descent can be three degree. What if you’re not sure which angle to use for a given scenario? Think of the AI as a protractor and treat zero pitch and 10-degrees nose low as your scale limits. Let’s say ATC instructs, “Cross HAZEE at 5000.” You’re at 9000 feet and eight miles from HAZEE. This means you must lose 4000 feet in eight miles. Four is 50 percent of eight. Mentally overlay this on the AI scale. Half of our notional scale limits—the 50-percent mark—is five degrees nose low. Decrease your pitch five degrees from level flight and you’re bore sighted. (In truth, this is a way to simplify finding the gradient of 500 feet per mile. I only mention this if you’re so inclined as to dig deeper.)
For a last example, you’re conveniently set up at 4000 feet AGL for a 12-mile straight-in approach. You guesstimate that “four to lose in 12 miles” is roughly 30 percent. Sighting 30 percent of your 10-degree protractor scale is three degrees nose low. Ah ha! If you were following earlier, you recognized my softball set-up. “Four to lose” tripled means that 12 miles are required for our target three-degree descent. You see, either way you attack the situation, it yields the same outcome.
Finally, understand that if you had to lose 5000 feet in five miles, that’s 100 percent, or 10 degrees nose low. Call that a one-for-one scenario. This is not a sustainable pitch for most airplanes. Reply to ATC with your best John-Wayne-cool and say, “Unable.”
There’s more to this discussion, but these are the basics. Even though no slide rule is required, these clear-cut techniques will score descent bulls-eyes. The NASA method is fine, but the Flying Tigers gun sight is so much more cockpit friendly and a pleasant way to “fly smarter, not harder.” — Ken Holston